Quantum Factoring Performance Evaluation - Using Parallel Programming - VB2010
The purpose of this document is to evaluate system performance in order to factorize large numbers in two prime numbers using Parallel Computing
The CPU evaluated is an a Intel Core i5 M 460 @ 2.53 Ghz.
The programming languages used is Visual Basic 2010. Parallel Processing is implemented using the BackGround Worker.
The Intel Processor used consists of two processors. Each processor is capable to handle 2 parallel threads. That means the Intel Processor consists of four processors. The name of the program is: "VB2010 FindPrim QC"
To perform the tests discussed in this chapter it is important that the PC does not go into sleepcondition. Select Configuration screen. Select Energy control. Select sleep condition. Select Never.
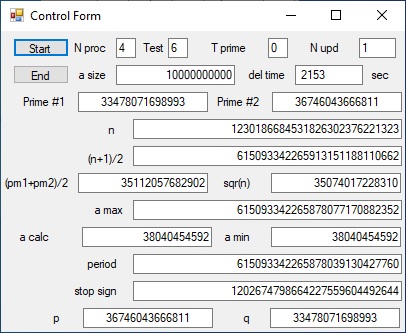
The current highest number factorized using 4 Processors is: 1230186684531826302376221323
The two prime numbers are: 33478071698993 and 36746043666811
Performance = 2153 seconds = 0 hours 35 min and 53 seconds
|
|
|
Picture 1 - Test = 6
|
When you compare the two prime numbers the difference is small. This has an advantage. See Reflection part 2
Performance evalution
The following table shows the perfomance evalution to factorize large numbers of different sizes using one, two three or four processors.
Intel Core i5 M 460 @ 2.53 Ghz.
| Test | 0 | 1 | 2 |
3 | 4 | 5 |
| pm1 | 33478079 | 334780717 | 3347807173 |
33478071761 | 334780716989 | 3347807169919 |
| pm2 | 36746063 | 367460449 | 3674604371 | 36746043727 |
367460436671 | 3674604366743 |
| amin | 38040 | 380405 | 3804046 | 38040455 |
380404547 | 3804045461 |
| a size | 10000 | 100000 | 1000000 | 10000000 | 100000000 |
1000000000 |
| pp = 1 | 0,051 | 0,101 | 0,595 | 5,257 | 52,279 | 507 |
| pp = 2 | 0,052 | 0,088 | 0,372 | 3,031 | 30,311 | 312 |
| pp = 3 | 0,056 | 0,095 | 0,430 | 3,515 | 34,905 | 344 |
| pp = 4 | 0,057 | 0,088 | 0,325 | 2,516 | 24,671 | 253 |
|
Table 1: VB2010 FindPrim QC
Intel Core i5 M 460 @ 2.53 Ghz.
| Test | 0 | 1 | 2 |
| stop sign | 19141383145 | 89146125164832112 | 1787540236663610903 |
|
Table 1a: VB2010 FindPrim QC - stop sign
In order to understand the program "VB2010 FindPrim QC" the user should study : Answer question 11 - Calculating Periodicity in 5 easy steps Specific study Example 4 and the concepts amax and amin. The difference between those two parameters is the period.
The Visual Basic "VB2010 FindPrim QC" program follows the same 5 steps.
- In test 2 the number to factorize n = 12301866871170953183 which consists of two prime numbers: pm1 = 3347807173
and pm2 = 3674604371. See Picture 2 below
Calculate (n+1)/2. This is 6150933435585476592
Calculate sqr(n). This is the number 3507401726
Subtract those two numbers. You get : 6150933432078074866. This is amax. This number is larger than the periodicity.
- Now calulate 2 ^ amax mod n or 2 ^ 6150933432078074866 mod 12301866871170953183.
You get : 1787540236663610903. This is the stop sign.
- Now calculate 2 ^ amin mod 12301866871170953183 = 1787540236663610903 (stop sign)
This is a "difficult" calculation. See below for more detail.
The value you should get is amin = 3804046
- Now subtract amin from amax. The value you get is 615093343274270820. That is the period.
Divide period by 2 or 615093343274270820 by 2. You get: 3075466716037135410. This is per2
Now perform 2 ^ per2 mod n or 2 ^ 3075466716037135410 mod 12301866871170953183. You get 3151404462955436851. This is y.
- Now perform GCD (y+1,n) and GCD(y-1,n). The results are the two prime numbers searched for.
However the last two steps can also be modified to get a much faster algorithm:
-
Add "amin" to sqsr(n). you get (pm1 + pm2)/2 = 3507401726 + 3804046 = 3511205772 = s/2
When you multiply this number by 2 you get pm1 + pm2 = s (sum)
You already have n. which is equal to n = pm1 * pm2.
- In order to calculate pm1 and pm2 to you to solve the following equation: (replace pm2 by pm)
- (s - pm)*pm = n or pm^2 - s*pm + n = 0
-
That means: pm = (s +- sqr(s^2 - 4 * n))/2 = s/2 +- sqr( (s/2)^2 - n)
You get pm = 3511205772 +- sqr(3511205772*3511205772 - 12301866871170953183)
and next = 3511205772 +- sqr(26699102155162801) = 3511205772 +-163398599
and finally pm1 = 3347807173 and pm2 = 3674604371.
The beauty of this algorithm is that you always get the correct result without any guessing.
What is also important is that GCD algorithm is not used.
|
Step 3 is the most time consuming calculation. In fact you have to perform a loop of 3804046 iterations
This loop consists of the following calculations.
a = 1: xn = 2
DO
a = a + 1
xn = xn * 2
if xn > 12301866871170953183 then xn = xn - 12301866871170953183
LOOP until xn = stop_sign
amin = a
In this particular case amin = 3804046.
What is important that this is generally speaking a very simple calculation. There is no division involved, which is very time consuming and the only multiplification is with a factor of 2.
- Suppose you want to perform this calculation in parallel simultaneous in 4 different processors.
That means that each processor should roughly perform 3804046/4 = 1000000 calculations.
That means processor 1 performs the calculations from 1 to 1000000. processor 2 from 1000001 to 2000000. processor 3 from 2000001 to 3000000. and processor 4 from 3000001 to 4000000. In this particular case Processor 4 will return the final result.
- When you study the calculation of amin you will see that each iteration depents on its previous result.
That means that the start calulation of xn in Processor 2 depents on the final value of xn in Processor 1.
The same that the start calulation of xn in Processor 3 depents on the final value of xn in Processor 2.
To solve this time delay the program starts with modular exponentiation. That means first the function 2 ^ a mod n is calculated. For processor 2 this is 2 ^ 1000001 mod n
The program for processor 2 now becomes:
end_pp = 0
a = 1000000:
calculate: xn = 2^a mod n
DO
a = a + 1
xn = xn * 2
if xn > 12301866871170953183 then xn = xn - 12301866871170953183
LOOP until a = 2000000 or xn = stop_sign or end_pp > 0
if xn = stop_sign then
amin = a
end_pp = 2
end if
The parameter end_pp contains the processor # which detected the "stop sign". The parameter end_pp also services as a command to terminate the other processors.
- In the above case the value of 1000000 is selected to test the optimum solution. The value of 1000000 is called the a size.That means in each processor only at the start modular exponentiation is performed.
In reality this optimum value of 1000000 for the parameter a size is not known.
In case a size is 500000 the following calculations are performed in parallel:
- First in processor #1 from 1 to 500000. In #2 from 500001 to 1000000. In #3 from 1000001 to 1500000 and in #4 from 1500001 to 2000000.
- Secondly in processor #1 from 2000001 to 2500000. In #2 from 2500001 to 3000000. In #3 from 3000001 to 3500000. In #4 from 3500001 to 4000000.
- In this particular case each Processor will perform two times modular exponentiation and Processor #4 will find the answer with a = amin = 3804046
-
In order to implement parallel programming the concept of BackGroundworker is used. In total three. That means one Processor services as a Master and the three BackGroundWorkers serve as a slave.
For more information about the BackGroundworker read this: Visual Basic 2010 Parallel Programming techniques
The first task of the Master is to Assign or activate each slave. After assignment the slave starts a program which performs an endless loop
Communication between the Master and each Slave is controlled by a state array.
Backgroundworker 1 uses state(2). Backgroudworker 2 uses state(3) etc.
"VB2010 FindPrim QC" Program source.
For the readers to try the program there is an executable available.
To load this excutable as a Zip file goto: VB2010 FindPrim QC.zip
"VB2010 FindPrim QC" Program Operation.
The program is build using 3 Forms: Control Form, Display Form and Monitor Form:
-
The Control Form
The Control Form consists of the following parameters:
- N Proc This parameter contains the number of processors to be used. The maximum value is 4.
- Test The parameter test contains the standard test to be performed. The maximum value is 6. If used the value the value should be entered first and after that the other parameters can be modified.
- T prime . This is the "Test Prime number" parameter. This parameter is automaticaly set when any of the two Prime numbers is modified. The parameter is used to test and to calculate the next Prime number.
- N upd This number is used to indicate the number of screen updates for each a_size. When the parameter "a size" is 100000 and N_Upd is 10 there is a screen update after every 10000 iterations.
|
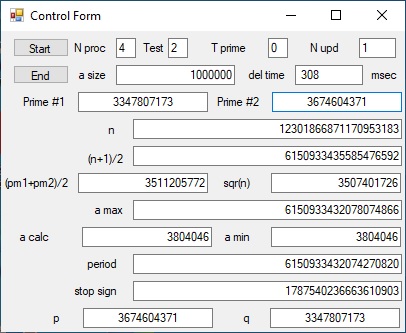 Picture 2 - Test = 2
Picture 2 - Test = 2
|
|
- a size This parameter is the buffer size. The value is calculated as a function of the parameter Test selected, to test optimum performance.
This value should be modified after the parameter Test is selected.
- Fr Back This is the "Test Front to Back" parameter. The value is normally zero.
When this parameter is set a special "Front to Back" test is performed as part of a divide operation. During divide operation then Dividend is divided by the Divisor to give the Quotient and a Remainder. That means Dividend/Divisor = Quotient en Remainder.
The Front to Back test performs the following task: Dividend = Quotient * Divisor + Remainder. If the test fails the program terminates.
- Prime #1 . This parameter is the first prime number tested. When this number is entered first a test is done if the number is odd. If it is not the number is increased with one. Next a test is done if it is a prime number. If it fails the test the number is increased with two until it passes the test.
- Prime #2 . This parameter is the second prime number tested. The test are identical as with Prime #1 .
|
The Control form contains the pushbuttons: Start, Stop or End
- When the Start pushbutton is selected first the two prime numbers are tested, Next the number n is calculated and all the numbers as explained in the beginning of this documment.
- When the Stop pushbutton is selected the program goes into the Stop state. The Stop pushbutton changes in End pushbutton. In general this functionality is difficult to perform if all the processors are busy.
- When the End pushbutton is selected the program terminates.
To Observe the performance of the program:
- Set N Proc to 4.
- Set Test to 3.
- Set N upd to 100.
- Select the the Start pushbutton.
- And Observe the Monitor Form
The program also works on a PC which only supports one Processsor.
-
The Monitor Form
The Monitor Form shows one pushbutton Monitor. When het Monitor pushbutton is selected the Monitor Form is updated. Normally this can be done after the end of a test to observe the final values.
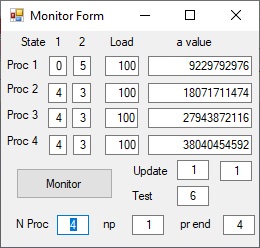 Picture 3 - Test = 6
Picture 3 - Test = 6
|
The Monitor Form shows the following 12 parameters:
- For each of the processors the parameters "State 1","State 2", "Load" and "a value"
The 2 parameter State values are: Free = 0, Start = 1, Active = 2, Finished = 3, Cancel = 4 and End = 5
The 2 parameter State are used to control the Backgroundworker.
- The parameter a value contains the actual value "a" to be used in each processor. The value depents on the Control Form parameter a size and the parameter N Upd
- The parameter Test shows the same value as the Control Form parameter N Test.
- The two parameter Update depend about the state of Processor 1 and the value of the Control Form parameter N Upd
- The first parameter displays the number of update cycles of processor 1 and is calculated based upon the parameter a size
- The second parameter is updated whenever the number
- The parameter N Proc is the same as the Control Form parameter N Proc but cannot be changed.
- The parameter np shows the actual number of Processors in use.
|
The parameter "a size"
Table 1 shows for Test = 2 that the parameter amin = 3804046 and a size = 1000000. The parameter N Upd = 10.
That means the Monitor display is updated after each 100000 iterations
In this particular case, the Monitor Display shows that each processor on average has performed roughly 820000 iterations.
Processor 1 has performed the most number of iterations = 857547 and Processor 3 the least number = 776264.
Processor 4 has detected the final value and shows amin
Table 2 below, shows the results for Test 3 and Test 4 and for different values of the parameter a size. The number of processors used is 4.
| a size | Test = 3 | N upd |
a size | Test = 4 | N upd |
| 10000000 | 2,531 | 1 |
100000000 | 24,671 | 1 |
| 5000000 | 2,531 | 2 |
50000000 | 24,452 | 2 |
| 4000000 | 3,062 | 3 |
40000000 | 30,186 | 3 |
| 2000000 | 2,562 | 5 |
20000000 | 24,749 | 5 |
| 1000000 | 2,828 | 10 |
10000000 | 27,202 | 10 |
| 500000 | 2,969 | 20 |
5000000 | 27,249 | 20 |
|
Table 2: 4 Processors
What Table 2 shows is that almost all the parameter values are identical except for the bottom line with "a size" = 500000 (Test 3) and "a size" = 5000000 (Test 4)
The reason is that in this particular case the final value is calculated in Processor #1, and this is the Processor which is the most busy.
To solve that Load sharing is used. This means that in the case of 4 Processors in Processor #1 70% is done and in the 3 other processors each 110%
| a size | Test = 3 |
| 10000000 | 82,248 |
| 5000000 | 89,917 |
| 4000000 | 107,725 |
| 2000000 | 90,226 |
| 1000000 | 102,845 |
| 500000 | 105,509 |
|
Table 3: 4 Processors
|
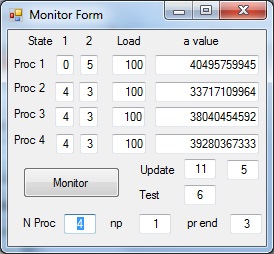 Picture 4 - Test = 6
Picture 4 - Test = 6
|
Table 3 includes Load Sharing The result is that now all the results are more or less identical.
Overview communication between Master and Slaves.
Communication between Processor #1 and Processor #2 (#3, #4) is controlled by the state arrays state1 and state2. The size is 4.
state 1 is used to send data from the master to the slaves
state 2 is used to send data from the slaves to the master
The state values are:Free = 0, Start = 1, Active = 2, Finished = 3, Cancel = 4 and End = 5
******* *****
* 1 * * 4 *
* * * *
state 1 **** ************************ ***********
************************ ***********
* 2 3 * * 5
* * *
state 2 ********** *****
period 1 2 3 4 5
|
Communication between Master and Slaves is controlled by 5 differents periods or events.
- Period 1 is identified that the operator enters the two prime numbers and the # of processors to be used and selects the Start pushbotton. If N Proc is 4 The 3 Slave processors are assigned and the Master issues start request. The state 1 array is set to 1.
- Period 2 is controlled by the "Back Ground Workers". The "Back Ground Worker" detects that state 1 is a Start request ( = 1 ) and issues a Active request. state 2 becomes a 2. The subroutines Geta_mod2_PP_x is started. (See also next paragraph).
- Period 3 is controlled by the subroutine Geta_mod2_PP_x. During its operation no communication with the master is required.
Period 3 can terminate in 2 ways.
- The master or slave detects the "stop sign". If that is the case the variable pr_end is set to the processor # of the master or slave.
- The master or slave detectects that the variable pr_end is not equal to zero.
in both cases the variable state 2 is set to finished. That means becomes 3.
subroutine Geta_mod2_PP_x is finished, but the Background worker is still active.
- Period 4 is controlled by the Master.
The first thing that the Master does is to test that all the processors go into the finished state. When that has happened the Master issues the Cancel Request and the array state 1 becomes 4.
- Period 5 is controlled by the "Back Ground Workers". The "Back Ground Worker" detects that state 1 is a Cancel request ( = 4 ) and issues a End request. state 2 becomes a 5. The "Back Ground Workers" ends.
This terminates all communication and the program.
Additional Software considerations.
Main_Int is central program, which runs in processor 1, that collects the input parameters, controls the three background workers, and calculates the final prime numbers.
Geta_mod2_PP is the name of the subroutine that calculates the periodicity. Main_Int uses Geta_mod2_PP
Geta_mod2_PP_2 is the name of the program which runs in parallel processor 2 and that also calculates the periodicity (part of).
Geta_mod2_PP_3 and Geta_mod2_PP_4 do the same either in processor 3 or 4.
Each of the programs Geta_mod2_PP has the same structure:
-
a call to the subroutine Modular_2_exp_Int_array and the execution of a loop.
within the loop the subroutine Test_Int_Simple_array is called.
Modular_2_exp_Int_array uses the following subroutines:
- Mul_Int_array to multiply two integer arrays.
- Mod_Int_array to calculate a Mod n.
-
This subroutine uses: Div_Int_Array
- Div_2_Int_array to divide an integer array with 2
- Add_Int_array to add two integer arrays.
The execution time of the loop is the most time consuming.
The subroutine Test_Int_Simple_array does not use any additional subroutines and can be easily copied inside the loop.
The type of mathematical operations used are: addition, subtraction and division by 2.
The integer array numbers used contain 9 digits. That means a number like 123456789123456789 is stored in two elements of an array.
The largest integer number for Intel R5 is 19 bits.
It is possible to work with larger integer numbers, but that is a typical programming exercise.
The program is written in Visual Basic 2010. It is possible to use an other language like C++. This is also a typical programming exercise.
Reflection part 1
Document Shor's Algorithm explains Shor's Algorithm in great detail. Reflection Part 5. - Cryptography. of that same document, shows Table 5 "CPU Performance P4". One line in Table 5 shows a value 29 in green. This whole line represents the same situation as in Test 2 in Table 1 above in this document. This is the Column with the value 28.943 in green . In both cases only one Processor is used.
What Table 1 demonstrates is that by using parallel processing the performance to do factorization can de drastically improved compared with the 1 Processor situation. This is a factor 4 when 4 Processors are used.
You can also describe this a little bit euphoric:
- The concept of parallel processing is the ultimum approach to simulate a PC as a Quantum Computer.
This concept leads to a much more general question:
-
Will a Quantum Computer using the concepts QBits, Superposition and Entanglement ever be able to outperform a PC?
-
I do not think it does.
In fact the difference in Performance between the two will only increase.
Reflection part 2
The two prime numbers pm1 and pm2 used to test are almost the same. In this paragraph we investigate what happens for different prime number combinations when the number n is almost the same.
The following table shows the result when prime number 1 becomes smaller and prime number 2 increases. The column dtime shows that processing time increases. Column update shows the number of screen updates, which increases because asize is constant. N proc = 4 and N upd = 1
| test | pm1 | pm2 | n | acalc/amin |
periodicity | dtime | update |
| 21 | 3450000017 | 3565758503 | 12301866895967894551 |
477530 | 6150933444476545546 | 0,172 | 1 |
| 22 | 3347807173 | 3674604371 | 12301866871170953183 |
3804046 | 6150933432074270820 | 0,312 | 2 |
| 23 | 3300000001 | 3727838447 | 12301866878827838447 |
6517497 | 6150933435900000000 | 0,531 | 2 |
| 24 | 3200000087 | 3844333357 | 12301867076857002059 |
14764967 | 6150933534906334308 | 1,016 | 5 |
| 25 | 3000000019 | 4100622271 | 12301866890911823149 |
42909416 | 6150933441905600430 | 3,359 | 13 |
| 26 | 2000000011 | 6150933427 | 12301866921660267697 |
568064986 | 6150933456754667130 | 41,186 | 143 |
| 27 | 1500000001 | 8201244581 | 12301866879701244581 |
1343220564 | 6150933435000000000 | 105 | 378 |
| 28 | 1000000007 | 12301866785 | 12301866871113067495 |
3143531670 | 6150933428905600352 | 1187 | 889 |
What the above shows is:
- that the number n in all the cases tested is almost identical.
- that the prime number in column 1 decreases and in column 2 increases.
- that the periodicity is almost identical.
- The parameter "acalc" and "amin" are identical. The parameter "acalc" can directly be calculated when the two prime numbers are known. "acalc" = (pm1+pm2)/2 - sqr(n).
"amin" is calculated as result of the simulation. What the table shows is that "amin" is increasing.
- That dtime is also increasing. dtime is the time in seconds. The reason is simple because the variable "a" services as a loopcounter.
The final value is called "amin" when the stopsign is detected. That means how more loops, how larger "amin" how larger "dtime".
Feedback
None
Created: 8 November 2013
Updated: 1 December 2015
Updated: 19 August 2021
Back to Shor's Algorithm - 10 Questions
Back to my home page Contents of This Document



